В реальной жизни вещи не бывают черными или белыми. В особенности это относится к ситуациям, когда накопление данных ведется с целью показать конкретную взаимосвязь между переменными. В тот момент, когда на основе наших наблюдений мы пытаемся выявить некую закономерность, модель, мы начинаем сомневаться в этих самых наблюдениях, поскольку нет ничего абсолютного (т.е., черного или белого). Ассоциативные модели весьма полезны, поскольку помогают сконцентрировать ресурсы – идет ли разговор о времени, финансовых средствах или о каком-то предполагаемом вмешательстве в процесс. Коэффициент вероятности (КВ) – это статистический/эпидемиологический инструмент, которым можно пользоваться, чтобы вскрыть взаимосвязь между двумя бинарными переменными. Вычисление КВ требует того, чтобы данные были представлены в виде таблиц 2 х 2, поэтому данные должны быть отформатированы категориальным образом (т.е., в виде «да» и «нет» для двух отдельных переменных).
Таблица 1. Общее представление данных в таблице вида 2 х 2

| Переменная 1 | |||
| да | нет | ||
| Переменная 2 | да | a | b |
| нет | c | d | |
С помощью Таблицы 1 (выше), КВ может быть посчитан простым перекрестным умножением и делением. Отсюда:
(a*d)
КВ= -----------
(b*c)
КВ хорош тем, что вам нет необходимости переживать за порядок используемых переменных (какая из них располагается сверху, а какая сбоку), поскольку результат вычислений будет тем же. Из вышеприведенной формулы понятно, что КВ будет всегда иметь положительное значение, а его результат будет лежать в диапазоне от нуля до бесконечности. Интерпретируем КВ следующим образом:
КВ<1 – указывает на «защитный» характер ассоциации, означая, что событие, скорее всего, не произойдет;
КВ=1 – говорит о том, что связь между двумя переменными отсутствует;
КВ>1 – показывает, что связь существует, при этом, чем выше значение, тем эта связь прочнее.
Для КВ также можно посчитать 95%-ный доверительный интервал, получив, таким образом, диапазон истинных ожидаемых значений. Формула не отличается такой уж сложностью. Ключевую роль здесь играет то, что если, при вычислении КВ в его 95%-ном ДИ, в интервал попадает его значение, равное «1», то это означает, что связь (ассоциация) не является статистически важной и результаты, таким образом, могут быть вызваны исключительно случайными причинами.
Необходимо подчеркнуть, что вычисления КВ не дают нам причины и следствия, они просто предполагают наличие связи. Например, люди с высоким ростом будут, скорее всего, носить брюки с более длинными штанинами, чем люди с невысоким ростом. Однако, существуют люди с невысоким ростом, которым, в силу каких-то личных причин, нравится носить брюки большой длины. Поэтому, хотя эти две переменные (рост и длина штанин) и связаны, это не означает, что просто купив штаны подлиннее, вы станете выше ростом (т.е., отсутствие обусловленности).
Для лучшего понимания того, как можно пользоваться КВ, чтобы вскрыть и продемонстрировать связь, давайте рассмотрим пару примеров с данными, взятыми из практики.
Пневмония и язва желудка
Один из моих коллег пытался разобраться, существовала ли, на их конкретном производстве, ассоциация между язвой желудка и пневмонией. Известно, что язва желудка может быть вызвана многими причинами. Возможно, изначально вопрос ставился таким образом: «Если мы выполним программу вакцинации против возбудителей респираторных заболеваний, поможет ли это сократить число случаев язвы желудка?». Несмотря на то, что многие были бы не прочь составить программу исследования, чтобы разобраться с этим вопросом, в «поле» первый вопрос должен быть другим. Этот первый вопрос, в данном случае, должен ставиться так: «В условиях нашего производства, существует ли связь между пневмонией и язвой желудка?». Это важный вопрос, поскольку, для того, чтобы существовала возможность влиять на результат, первым делом необходимо, чтобы имела место связь. При этом, снова вспомним, что наличие связи не показывает и не подтверждает обусловленность. Тот факт, что пневмония и язва желудка ассоциированы в данной конкретной системе (на данном предприятии), совсем не означает, что, предотвращая пневмонию, обязательно удастся сколько-нибудь существенно сократить количество случаев язвы желудка (обусловленность).
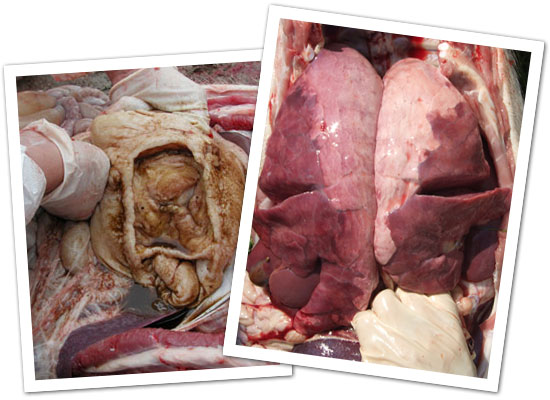
По результатам вскрытия 812 свиней были получены следующие данные:
у 336 (41,3%) свиней была язва/гиперкератоз;
у 600 (73,9%) свиней была пневмония;
у 290 (35,7%) свиней были язва/гиперкератоз И пневмония;
у 166 (20,4%) свиней не было ни того, ни другого.
Расшифровать такие данные весьма проблематично, поэтому они были сведены в таблицу вида 2 х 2 (Таблица 2.). С помощью формулы для КВ, получили:
(290*166) 48.140
КВ = ---------------- = ------------ = 3.38
(46*310) 14.260
Таблица 2. Взаимосвязь между пневмонией и язвой или гиперкератозом у 812 свиней.
| Язва/гиперкератоз | |||
| да | нет | ||
| Пневмония | да | 290 | 310 |
| нет | 46 | 166 | |
Это означает: шансы на то, что у свиней, у которых есть пневмония есть также и язва/гиперкератоз, в 3,38 раза (95%ДИ, 2,35 до 4,87) выше, чем у тех, у кого ее нет. Можно также сказать, что у свиней с язвой/гиперкератозом в 3,38 раз выше вероятность того, что у них есть также и пневмония. Ввиду того, как КВ вычисляется, ассоциация между пневмонией ⇔ язвой/гиперкератозом работает в обоих направлениях. Поскольку в наш 95%ДИ не содержит значения, равного 1, делаем вывод, что данный КВ является статистически значимым (связь, скорее всего, не возникла исключительно случайно). Теперь, зная, что между пневмонией и язвой/гиперкератозом существует связь, мы можем быть уверены в том, что возможность суметь повлиять на результат существует. Теперь можно тратить время и материальные ресурсы на то, чтобы провести исследование и увидеть, поможет ли проведение вакцинации против возбудителей респираторных заболеваний снизить число случаев язвы желудка.
Диарея у ремонтного молодняка и у поросят
случае клиент обратил внимание на то, что у 3-дневных новорожденных поросят участились случаи диареи. Винил он в этом свой новый источник поступления ремонтного молодняка, с которым на ферму был занесен новый возбудитель. Маточное поголовье составляло 1250 голов. В день проведения осмотра поголовья было обнаружено, что в 17 из 58 (29,3%) пометов только что вспыхнула диарея. Проводя осмотр помещений с диареей, вы видите, что есть много пометов ремонтных свинок с диареей, но также диарея есть и в нескольких пометах более старых свиноматок. Вы составляете вашу таблицу вида 2 х 2 (Таблица 3) и рассчитываете ваш КВ = 14 (ДИ 95% = 3,6 : 54,3). В данном случае, в 14 раз выше вероятность того, что поросята с диареей получены от ремонтных свинок, а не от «старых» свиноматок, и это не простое совпадение (т.е., это статистически значимо). Если бы новый ремонтный молодняк занес на ферму новый патоген, КВ указал бы на поросят от «старых» свиноматок, поскольку те с ним до этого не встречались. У вас же есть веское доказательство того, что, по факту, больше баллов набрали поросята от ремонтного молодняка, т.е., более вероятно, что это ремонтный молодняк столкнулся с чем-то, с чем раньше не сталкивался и что, скорее всего, уже присутствовало на ферме. Таким образом, принимая оперативные меры, начинать нужно именно со спасения ремонтных свинок, а не остального маточного поголовья.
Таблица 3. Связь между диареей у поросят и номером опороса (свинки vs остальные).
| Диарея поросят | |||
| да | нет | ||
| Рем.свинки | да | 12 | 6 |
| нет | 5 | 35 | |
Суммируя: КВ – отличный инструмент, который в полевых условиях способен помочь квантифицировать прочность связей между двумя дихотомными (бинарными) переменными. Чем сильнее эта связь (читай, чем больше значение КВ), тем больше вероятность, что изменение одной переменной повлечет за собой изменение второй переменной. Если же вы захотите определить, какое воздействие окажет такое изменение, тогда вам потребуется вскрыть обусловленность (причинно-следственную связь), а также для каждой переменной посчитать атрибутируемый риск.



